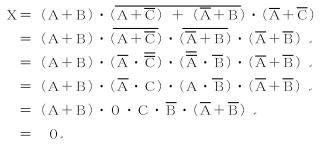既出設問パターンの概要把握と攻略研究
問題3 論理回路ほか
使える基本的な実力?
その1 ベン図 ⇒ ブール代数
その2 2進数 の計算
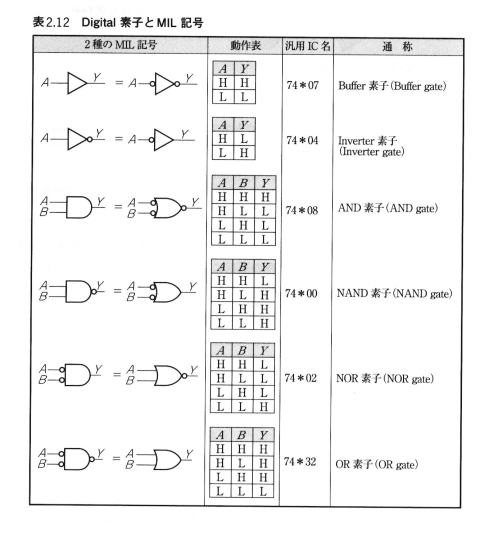
その3 論理素子
その4 FF(フリップ・フロップ)が含まれる回路 ⇒ タイミングチャート
既出問題の頻出度合の分析
毎回,4問(各5点 計20点)が出題
論理式や論理シンボル,2進数等を用いた計算問題が4問
設問の形態がほぼ一定。
基礎の基礎および,設問固有のコツをしっかり把握できていれば回答容易。
但し,設問固有のコツが理解できるまでは難問に見えるかも。
| 【問題3】の全容 | 配点 | R02 2020 |
H31 2019 |
H30 2018 |
H29 2017 |
H28 2016 |
H27 2015 |
H26 2014 |
H25 2013 |
H24 2012 |
H23 2011 |
|||||||||||
| 20点 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | 2回 | 1回 | ||
| ベン図 論理積または論理和 ⇒ 論理式 選び |
5点 | ● | 中止 | ● | ● | ● | ● | ● | (d) | (e) | (f) | ● | ● | 『ベン図』, 『2進数の計算』, 『論理素子の穴埋め』から2問が出題される。 |
||||||||
| 2進 論理積または論理和 ⇒ 10進 or 2進 |
加算 | (a) | 乗算 | 加算 | 加 算 |
(a) | (b) | (c) | ● | ● | ● | ● | ||||||||||
| 論理素子 穴埋め タイミングチャート or 論理式 |
5点 | ● | ● | ● | (g) | (h) | (i) | (j) | (k) | (l) | ● | ● | ● | ● | ● | ● | ||||||
FF タイミンチャート選び |
5点 | 毎回出題 別表参照(new) | 『こつ』さえわかれば 【サービス問題】 に見えるはず |
|||||||||||||||||||
ブール代数 簡略化 |
5点 | ● | ● | ● | ● | ● | ● | ● | (t) | (u) | (v) | (w) | (x) | (y) | ● | ● | ● | ● | ● | ● | 基本方式の理解と 活用力が問われる |
|
計算問題の回答に許される時間は, 3分/問 以下・・・この力をつけるのが必須。

↑某サイトから勝手にコピー・・・しばらく使わせてください。
↑CQ出版社 デジタル・システムの設計
興味のある方は是非手に取って見てください(宣伝)
左右に並んだロジックシンボルは,全く同じ動作をします。
H=1,L=0のこと
以下の問題集の使用法について
問題3の過去6回(3年)分を整理した。
・ 市販参考書を見ても理解困難な場合
迷わず ⇒ 誰か(先輩・有資格者)に聴く。
※要するに,わからない状態で悶々とした状態を引きずらないこと!
時間の無駄のみでなく,やる気が著しく消耗し,挫折します。
・ 解き方が理解できたら、
何も見ないで解ける回数を増やします。
最終的には,
3分~2分台で解ける速さも目標です。
・・・くどいようですが,速さ・正確さが大切です。
⇒ 10進 or 2進
H28(2016)#2 問題3-(1)


題意のチェック
① 『乗算』という文字にチェック
②
にアンダーラインを引き,2進数のどの部分を回答する。
・・・これが一番重要。
解き方
③ X1とX2を10進数に置き換えてX0を求める(10進)
④ X0を2進数に変換
⑤ 問題が指定している先頭から2、3,4番目の数値を
答える

① 『加算』という文字にチェック
②
にアンダーラインを引き,2進数のどの部分を回答する。
・・・これが重要。
解き方
③ X1,X2,X3を10進数に置き換えてX0を求める(10進)
④ X0を2進数に変換
⑤ 問題が指定している先頭から4,5,6番目の数値を
答える

① 『加算』という文字にチェック
②
にアンダーラインを引き,2進数のどの部分を回答する。
・・・これが重要。
解き方
③ X1,X2,X3を10進数に置き換えてX0を求める(10進)
④ X0を2進数に変換
⑤ 問題が指定している先頭から3,4,5番目の数値を
答える
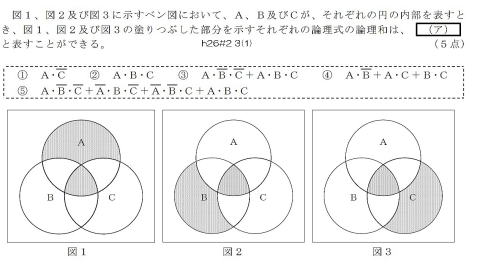
⇒ 論理式 選び
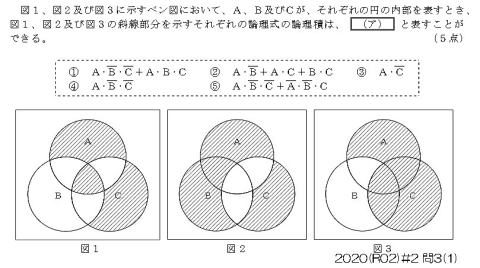
① 『論理積』という文字にチェック
② 図1の網掛け部分に,
図2・図3ともに重複する部分を,鉛筆でマーキング
③ 鉛筆でマーキングした部分を表す,論理式を探す
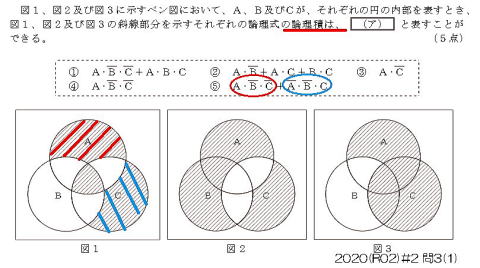
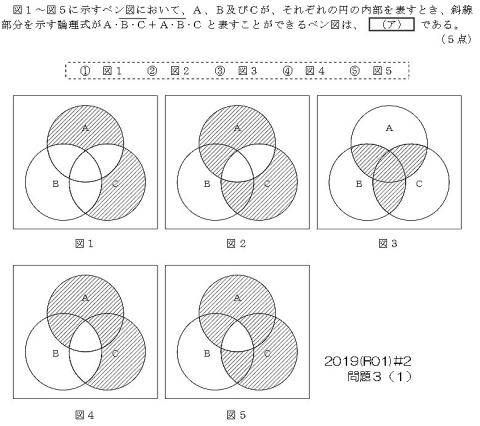
回答手順
①論理式をじっくり眺める
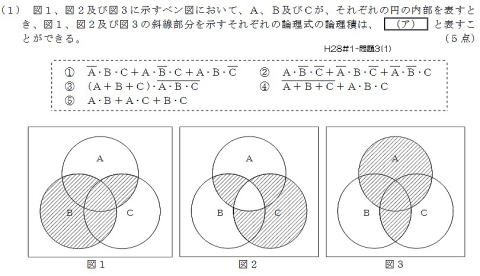
① 『論理積』という文字にチェック
② 図1の網掛け部分に,
図2の網かけ部分と重複する部分を,鉛筆でマーキング
図3の網かけ部分と重複する部分を,鉛筆でマーキング
③ 鉛筆でマーキングした部分を表す,論理式を探す
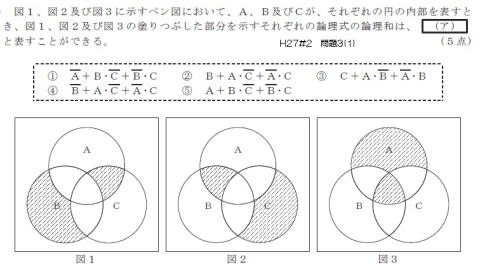
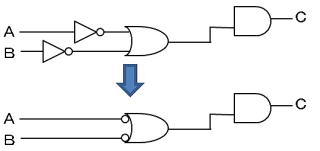
① 『論理和』という文字にチェック
②
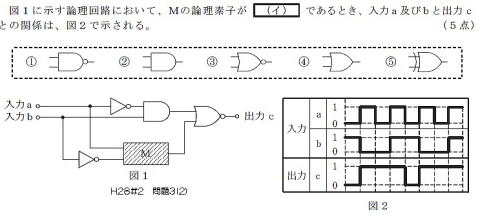
タイミングチャート or 論理式
H28#2
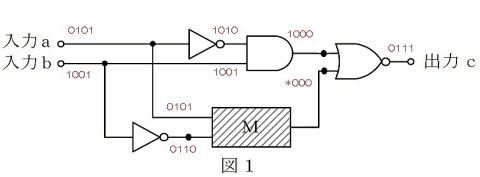
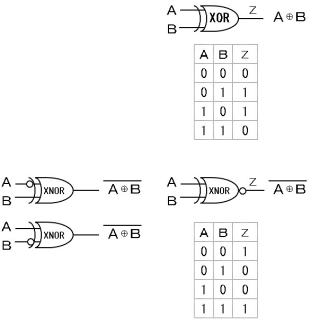
示された論理式はEXOR
下半分のゲート回路はHH⇒H
上半分のゲート回路でも
HH⇒H
L L⇒H 動作をすれば
NORゲートの出力は
HH⇒L
LL ⇒L
HL⇒H
LH⇒H となる・・・
(参考)
追記:2017/02/11
h27#2 3(2)
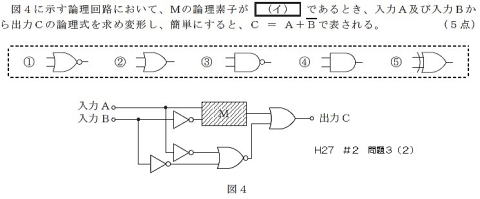
A,BがともにhighのときHigh
ゆえに
上半分では,A+/Bを満足する必要がある
これから
答えは②
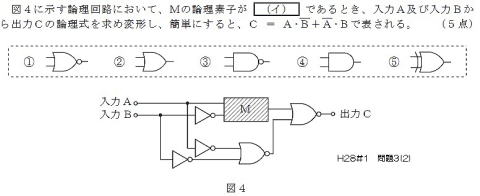
2018(H30)#2
2015(H27)#1
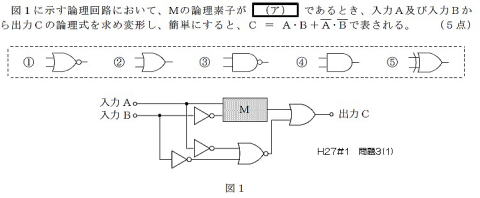
論理が合うように変換すると
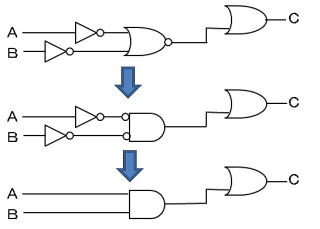
ド・モルガンの変換を用い,シンボル間の
論理を合わせると,回路がシンプルに・・・
C=A・B
上半分のゲート回路で
/A ・ /B または
/A ・ /B+ A・B を満足できれば良い
従って,答えは⑤
(参 考)
ORやAND,NORやNANDは,
真理値表を忘れても
シンボルから挙動が直接的にイメージできる。
EXORやEXNORだけは
真理値表を忘れてはいけない・・・!
イクスールシブ・オア・・・排他的論理和・・・・・
イクスルーシブ・ノア・・・一致(否定排他的論理和)・・
イクスルーシブ・オアの3端子のいずれか
にインバータを付加すると,この動作をする。

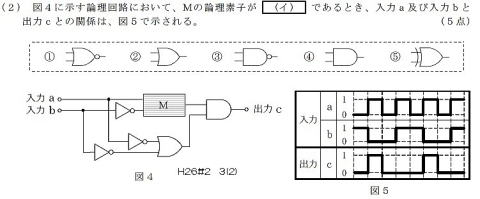
図4の下半分は,
A,BどちらかがLowのときHigh
上半分には, Aがhigh and Bがlow
BOX-M には、
④が入る
| 入力a | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 入力b | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
| M上側入力 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
| M下側入力 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 出力c | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
BOX-MにはEXORが入る
記:2017/02/11
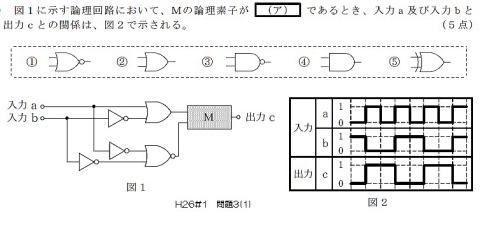
出力nのタイミンチャート選び
最近はNANDゲートによるFF回路の出題が続いている、
NORゲートによるFF回路も、臆することはありません。
基本知識と,攻略手順さえ知っていれば,容易に解けます。
基礎知識その1:タイミングチャート,ビット列の表現のしかた
基礎知識その2:NANDやNORの真理値表の特徴
※さらに出題される,FFの入力のビット列の特徴
※正攻法にこだわる方は,市販参考書で勉強してください。
※正攻法はどうでもいい・・・なんとか答えを出したい方は,以下に紹介する
解き方で挑戦してください。
| R03 2021 |
R02 2020 |
R1,H31 3019 |
H30 2018 |
H29 2017 |
H28 2016 |
H27 2015 |
H26 2014 |
||||||||||||||||||||||||||||
| #2 | #1 | #2 | #1 | #2 | #1 | #2 | #1 | #2 | #1 | #2 | #1 | #2 | #1 | #2 | #1 | ||||||||||||||||||||
| 例1 | 中 止 |
● | ● | ||||||||||||||||||||||||||||||||
| 例2 | ● | ||||||||||||||||||||||||||||||||||
| 例3 | ● | ● | |||||||||||||||||||||||||||||||||
| 例4 | ● | ||||||||||||||||||||||||||||||||||
| 例5 | ● | ||||||||||||||||||||||||||||||||||
| 例6 | ● | ||||||||||||||||||||||||||||||||||
| 例7 | |||||||||||||||||||||||||||||||||||
例1~例3に分類してはみましたが,解き方は一緒。 したがって,このパターン分析はあまり意味ないですね。
2016(H28)問題#2 問題3-(3) 出力cを ①~⑥から選ぶもの
2017(H29)問題#1 問題3-(3) 出力dを ①~⑥から選ぶもの
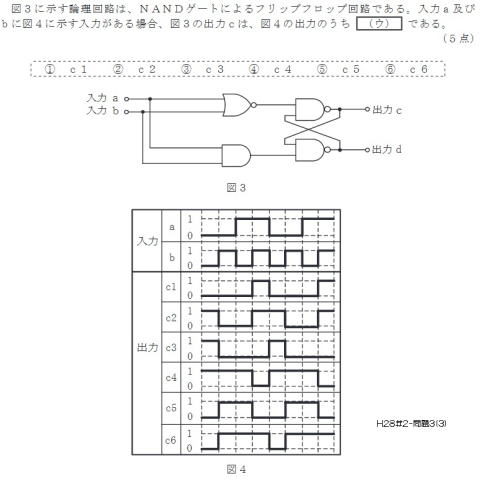
2016(H28)#2
step1:出力cを出力している
上側のNANDの入力端子のタイミング
チャート(=上側NORの出力)を導き出す
step2:見ての通りに変換
して出力cを得ます。 答え⑥c6
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 上のNOR の出力 |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 出力c | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
2017(H29)#1
step1:出力dを出力している
下側のNANDの入力端子のタイミング
チャート(=下のAND出力)を導き出す
step2:見ての通りに変換
して出力dを得ます。 答え④c4
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 下のAND の出力 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 出力d | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
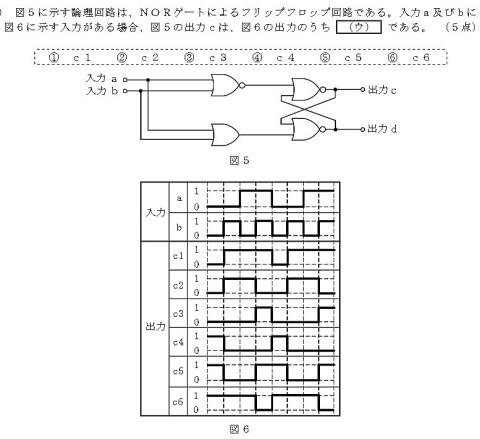
step1:出力cを出力している
NORの上側の入力端子のタイミング
チャート(上側のNOR出力)を導き出す
step2:見ての通りに変換
して出力cを得ます。 答え①c1
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 上のNOR の出力 |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 出力c | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
H30#1 問題3-(3)
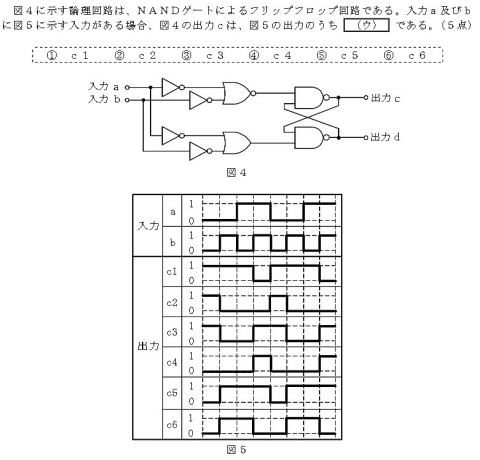
step1:出力cを出力している
上側のNANDの入力端子のタイミング
チャート(=上側NORの出力)を導き出す
step2:見ての通りに変換
して出力cを得ます。 答え③c3
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 上のNOR の出力 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 出力c | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
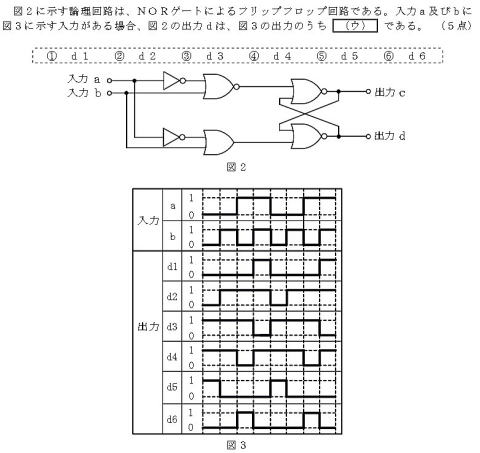
step1:出力dを出力している
下側のNORの入力端子のタイミング
チャート(=下のOR出力)を導き出す
step2:見ての通りに変換
して出力dを得ます。 答え⑥d6
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 下のAND の出力 |
1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 出力d | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
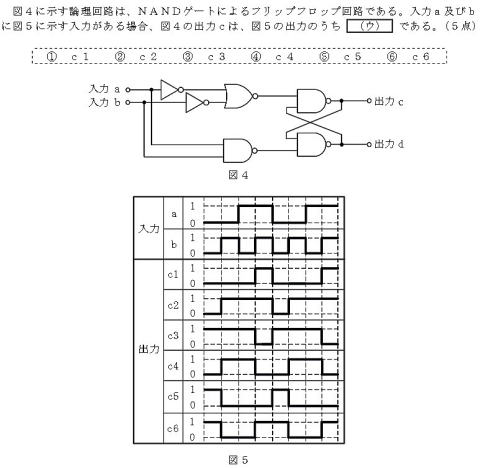
上側のNANDの入力端子のタイミング
チャート(=上側NORの出力)を導き出す
step2:見ての通りに変換
して出力cを得ます。 答え③c3
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 上のNOR の出力 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 出力c | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
記:2020/12/14
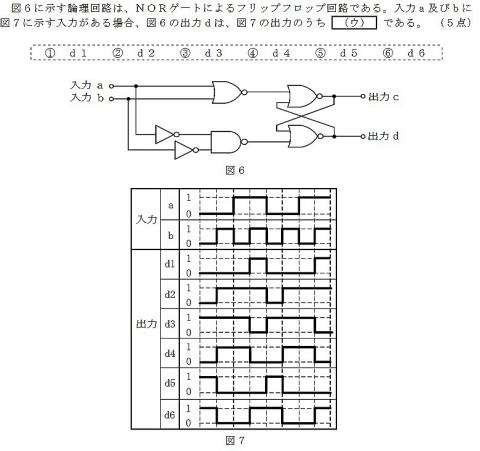
step1:出力dを出力している
下のNORの入力端子のタイミング
チャート(=下側NANDの出力)を導き出す
step2:見ての通りに変換
して出力dを得ます。 答え⑤d5
| 入力a | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 入力b | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 下のNAND 出力 |
0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 出力d | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
記:2020/12/19

2016(H28)#1
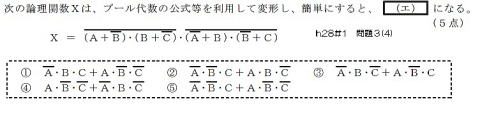
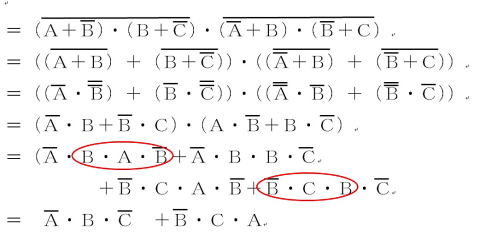

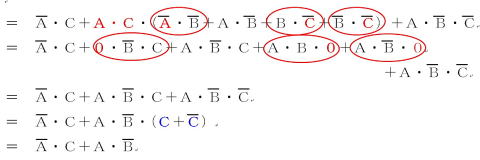

2012(H24)#2



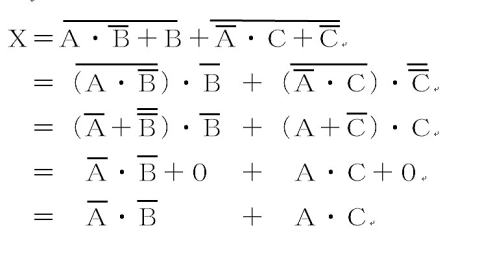

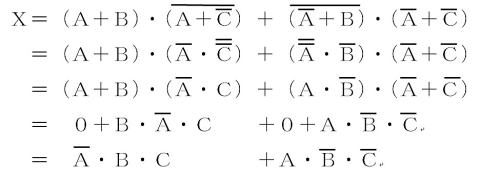

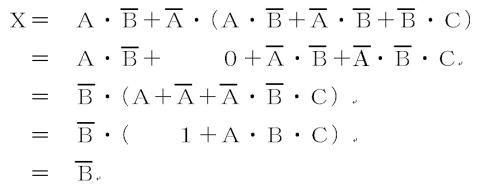

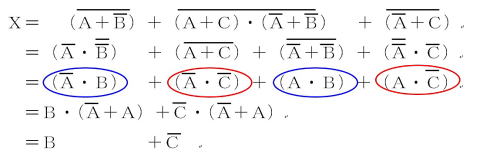
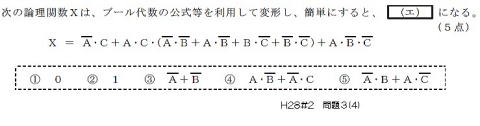
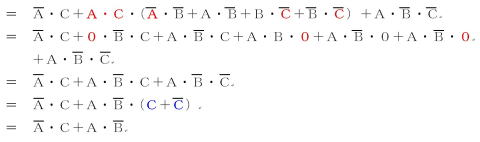
よって答えは,⑤
2016(H28)#1

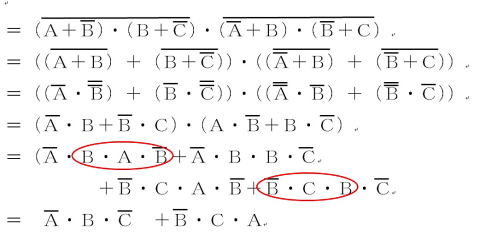
よって答えは,③